Arquivos Maxwell - Página 2 de 2 - Laboratório Maxwell

#LABMAX tem trabalho de pesquisa PREMIADO no ENCOM 2016

Trabalho de pesquisa do Laboratório Maxwell, baseado em uma melhoria da antena Palm Tree, foi premiado como um dos melhores trabalhos apresentados na última edição do ENCOM 2016, que é o Encontro Anual do Iecom em Comunicações, Redes e Criptografia.

Para a alegria dos pesquisadores do Laboratório Maxwell do IFSP e aproveitando a atenção acadêmica a nós direcionada, vamos divulgar prontamente que acabamos de receber o CERTIFICADO de melhor trabalho apresentado neste proeminente congresso.

O ENCOM 2016 foi realizado, nos dias 7, 8 e 9 de outubro de 2016, na Universidade Federal do Ceará (UFC) e no Instituto Federal de Educação, Ciência e Tecnologia (IFCE), em Fortaleza, Ceará, com o apoio da Universidade Federal de Campina Grande (UFCG), e contou com a presença de renomados palestrantes nacionais e internacionais.

O ENCOM 2016 teve por intuito congregar os maiores pesquisadores, bem como, estudantes, professores, empresários e profissionais das áreas de comunicações, telemática, redes de computadores, informática, criptografia e do mercado de telecomunicações para proporcionar a discussão de pesquisas e soluções de assuntos correlatos a comunicações.

A Palm Tree AVA, cujo artigo publicado na IEEE Antennas and Wireless Propagation Letters está disponível clicando aqui, é uma antena antipodal Vivaldi diretiva. Para aumentar ainda mais o ganho do lóbulo principal, uma lente de substrato e um diretor metálico foram adicionados de maneira a controlar ainda mais sua radiação.

Observe no diagrama de distribuição de campos elétricos a 6 GHz da Palm Tree AVA que há mais diretividade que a AVA convencional, cujo diagrama é apresentado na sequência.

Distribuição de Campos Elétricos da Palm Tree AVA com Lente de Substrato e Diretor Metálico a 6 GHz.

Distribuição de Campos Elétricos da AVA convencional a 6 GHz.

Os autores do artigo são os doutores:

Alexandre Charles Perotoni Justo Takeo

ARTIGO COMPLETO

porDr. Alexandre

Início do Curso de Extensão de Eletromagnetismo Aplicado no próximo dia 21

Inicia-se na próxima quarta (21) o Curso de Extensão de Eletromagnetismo Aplicado. Este curso tem por finalidade desenvolver as habilidades de análise, abstração, identificação e resolução de problemas tecnológicos a partir do uso de Eletromagnetismo Aplicado.

porDr. Alexandre

Episódio Piloto do estudo aplicado do Eletromagnetismo

Foi ao ar, no dia de hoje, 4 de setembro, o episódio piloto de um programa que contará com diversos episódios tratando de forma didática os fenômenos do Eletromagnetismo.

Este projeto chamado Um Passeio pelo Eletromagnetismo é uma produção do Laboratório Maxwell e trará como apresentadores, os pesquisadores do laboratório.

Este episódio foi gravado no estúdio da Rádio Federal e aborda a primeira equação de Maxwell, na forma integral, da lei de indução de Faraday dando origem a compreensão das tensões e correntes alternadas.

Por tratar-se de um episódio piloto, fique bem a vontade para enviarmos suas sugestões e críticas de maneira a nos ajudar a difundir a ciência e a educação com excelência em qualidade.

Diga-nos sua opinião sobre esse episódio piloto.

porDr. Alexandre

Antena, Equações de Maxwell, Projeto

Projeto de Antenas Assistido pelo Computador

No passado, os projetistas de antenas observavam a mesma dificuldade que hoje nós temos, no que tange ao projeto de antenas, encontrar o melhor desenho que proporcione a radiação dos campos eletromagnéticos.

E como era realizado o projeto de uma antena no passado? Ótima questão, mas antes de tentar respondê-la, é preciso definir o que é uma antena!

Segundo o dicionário Webster’s, uma antena pode ser definida como “a usually metallic device (as a rod or wire) for radiating or receiving radios waves” ou seja, é um dispositivo, geralmente metálico (uma haste ou um fio), para irradiar ou receber ondas de rádio. Já para o Standard Definitions of Terms for Antennas (Definições Padrões dos Termos para Antenas) do IEEE – Institute of Electrical and Electronics Engineers (Instituto de Engenheiros Eletricistas e Eletrônicos), uma antena pode ser definida como “a means for radiating or receiving radio waves“, ou seja, um meio para irradiar ou receber ondas de rádio [1].

Para Balanis (2016) [2], uma antena é uma estrutura de transição entre o espaço-livre e um dispositivo guia (de ondas eletromagnéticas).

Para entendermos estas definições, vamos imaginar um circuito transmissor (TX) de ondas de rádio, ligado por uma guia de ondas (Guia de ondas, cabo coaxial ou cabo par trançado) a outro circuito, neste caso o receptor (RX), Fig. 1. O sinal de radiofrequência (RF) é gerado pelo TX, enviado pela guia de ondas e recebido pelo RX.

g78657

Figura 1 – Exemplo de comunicação eletromagnética por ondas de radio frequência (RF) entre o circuito transmissor (TX) e o circuito receptor (RX) através de uma guia de ondas. Representação vetorial da onda eletromagnética propagada.

Agora imagine que TX está suficientemente distante de RX, a ponto de inviabilizar o uso de guia de ondas. Neste caso, usa-se uma antena para acoplar a guia de onda do circuito TX ao ar (Antena transmissora) e outra antena para acoplar o ar a guia de ondas do circuito RC (Antena receptora), como ilustra a Fig. 2. Nesta representação a onda eletromagnética, no meio (ar), é formada praticamente apenas pelos campos elétricos e magnéticos.

g78356

Figura 2 – Exemplo de comunicação eletromagnética por ondas de radio frequência (RF) entre o circuito transmissor (TX) e o circuito receptor (RX) através do uso de antenas.

Aplicações das Antenas.

As antenas podem ser aplicadas para as mais variadas tarefas. Por exemplo, para realizar uma transmissão de broadcast (difusão de sinal para todas as direções) é recomendado o uso de uma antena omnidirecional, por exemplo as antenas do tipo mono-polo, usadas em comunicadores de uso pessoal, como ilustra a Fig. 3.

radio

Figura 3 – Radio comunicador Intelbras [3].

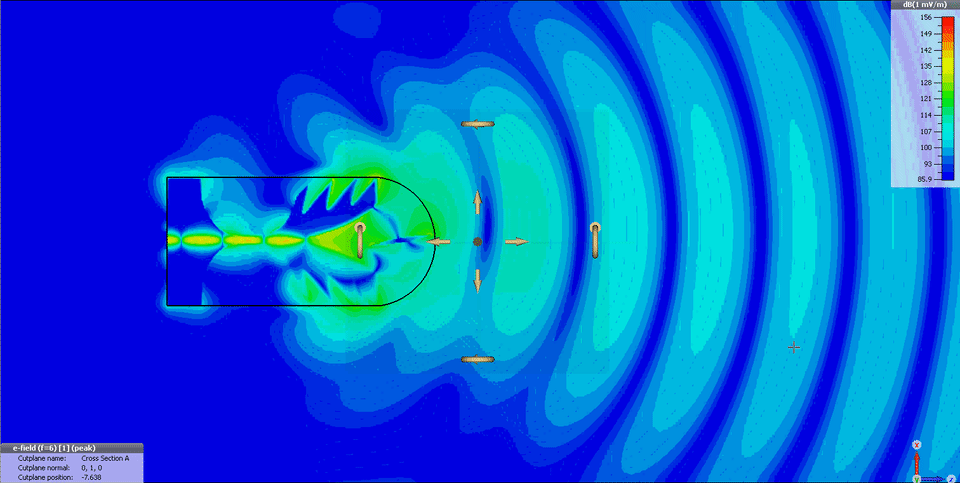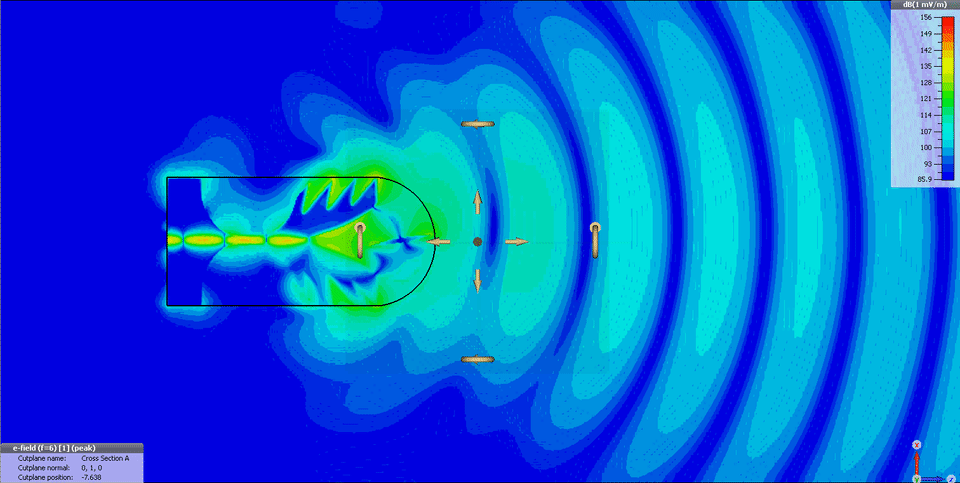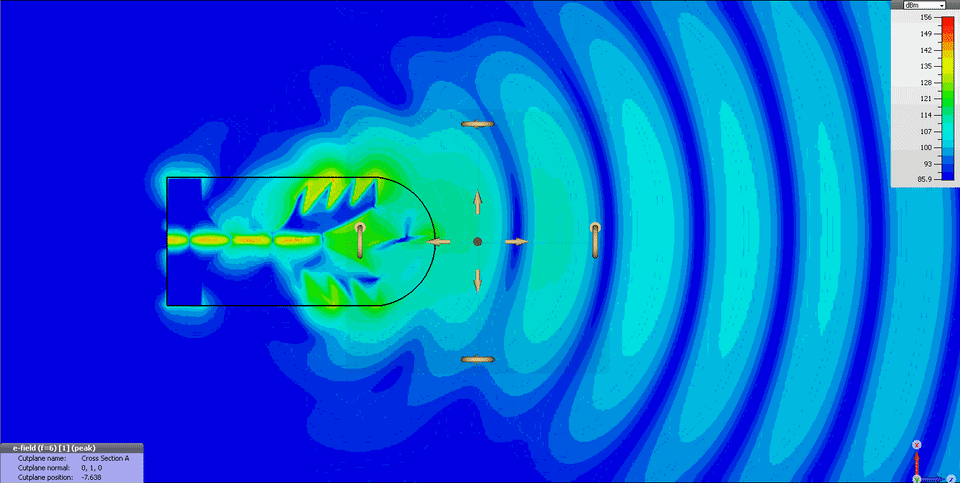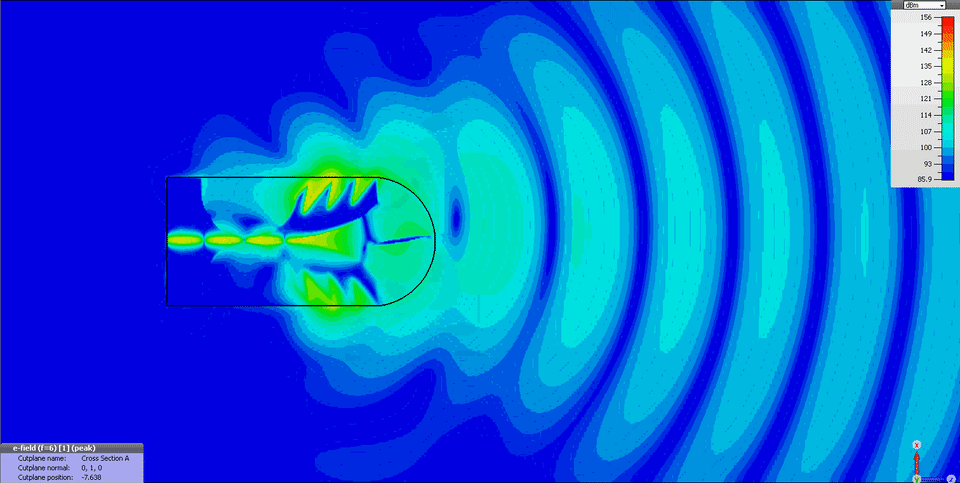
Já para aplicações de imagens médicas por micro-ondas, recomenda-se o uso de antenas direcionais, por exemplo do tipo Vivaldi Palm Tree [4], como ilustra a Fig. 4.

V974_reso_000graus_16GHz

Figura 4 – Diagrama de campos elétricos radiados da antena Vivaldi Palm Tree proposta por De Oliveira, et. al, 2015 [4].

Assim sendo, há um enorme e variado leque de opções de antenas diferentes, e todas elas possuem características específicas e precisara de um exaustivo projeto para chegarem a ser produzidas.

Projeto de antenas Assistido pelo Computador

No passado, na ausência de sistemas computacionais para projeto de antenas, como por exemplo o CST Microwave Studio TM, o HFSS, ou o ADS, os projetistas eram obrigados a adotar uma metodologia empírica de prototipação, sobretudo orientada a tentativa e erro, para determinar os vários parâmetros que constituem uma antena podem ser ineficientes e/ou dependerem da experiência do projetista.

Hoje, o projeto de antenas se dá em duas etapas: Primeiro é realizado o projeto em ambiente computacional e só depois é realizado a etapa de prototipação, uma vez que em sistemas computacionais, os testes são seguros, não expondo o projetista, ou mesmo os equipamentos a riscos desnecessários.

Na área do estudo dos efeitos do eletromagnetismo, pode-se citar o artigo “Finite Elements Solution of Saturable Magnetic Fields Problems” de Silvester e Chari (1970) [5] como um dos precursores, embora não o primeiro, da utilização do método de elementos finitos (Finite Element Method – FEM) para o desenvolvimento de resoluções de problemas eletromagnéticos, incluindo os de comportamento não linear.

Atualmente os programas de simulação eletromagnética usam várias técnicas de cálculo numérico para solucionar os problemas propostos. Um destes programas é o CST Microwave Studio, que usa a técnica de integração de elementos finitos (Finite Integration Technique – FIT) (CST, 2011) [6].

Técnica de integração de elementos finitos

Proposto inicialmente por Weiland em 1976 [7], o método numérico da técnica da integração elementos finitos, base do simulador eletromagnético de propósito geral CST Microwave 2011 utilizado nesta dissertação, fornece um método universal de discretização espacial aplicável a problemas eletromagnéticos de diversas naturezas, podendo ir de cálculos de campos estáticos à aplicações de alta frequência, tanto no domínio do tempo como no domínio da frequência (CST, 2011) [6].

Segundo as referências (CST, 2011; CLEMENS, WEILAND, 2001; WEILAND, 1996), o métodos numérico FIT discretiza na forma integral as equações de Maxwell, em vez da diferencial [8]:

fit01

(1)

fit02

(2)

fit03

(3)

fit04 (4)

Para resolver numericamente estas equações, o programa define um domínio finito de cálculo onde é confinado o problema a ser resolvido; cria-se então um sistema de malha (mesh) tridimensional através da divisão do domínio em pequenos elementos (grid cells) (CLEMENS; WEILAND, 2001). Uma segunda malha ortogonal à primeira é criada. A discretização tridimensional das equações integrais de Maxwell é efetuada com base nos dois sistemas de malha ortogonal como mostra a Figura 5 (CST, 2011; WEILAND, 1996).

fit05

Figura 5 – Discretização do domínio do problema eletromagnético em malhas ortogonais (CST, 2011; WEILAND, 1996).

Os campos elétricos tangenciais (e_i) e o fluxo magnético perpendicular (b_j) são alocados na primeira malha enquanto os campos magnéticos tangenciais (h_i) e o fluxo elétrico perpendicular (d_j) são alocados na segunda malha. Feito isso, aplicam-se as equações de Maxwell para cada uma das superfícies do hexaedro (CST, 2011; WEILAND, 1996).

fit06

Figura 6 – Ilustração das etapas de aplicação das equações de Maxwell nas faces do hexaedro (CST, 2011; WEILAND, 1996).

Com base na Lei de Faraday, a integral de linha pode ser reescrita como a soma das quatro tensões da malha sem introduzir erros suplementares além dos erros da discretização. Em seguida, a variação do fluxo magnético, definido ortogonalmente na face em questão, é representada pela derivada temporal do fluxo magnético que é equivalente a soma das tensões realizada anteriormente. Repetindo o procedimento para todas as faces disponíveis, incluindo a segunda malha, obtém-se o conjunto completo de equações de Maxwell na forma matricial (EGM) (CST, 2011; CLEMENS; WEILAND, 2001; WEILAND, 1996).

Deve-se salientar que a discretização espacial por um algoritmo numérico pode provocar instabilidade após muitas iterações. Entretanto a CST, (2011) afirma que com base nas relações fundamentais apresentadas, pode-se mostrar que o método FIT não afeta a estabilidade, pois o conjunto de EGM mantém a energia e conservação de carga (CST, 2011; WEILAND, 1996).

Finalmente, são aplicadas as relações materiais. Tais relações apresentam uma inevitável imprecisão numérica, devido ao processo de discretização espacial. Ao se definir as relações entre tensões e fluxos, seus valores integrais são aproximados ao longo das bordas da rede e as áreas das células, respectivamente. Consequentemente, os coeficientes resultantes dependem dos parâmetros dos materiais envolvidos, bem como sobre a resolução espacial da malha, resultando em suas matrizes correspondentes (BARTSCH, 1992) [9].

Todas as equações na forma matricial estão disponíveis para resolver problemas eletromagnéticos, de forma discretizada em malhas tridimensionais (CST, 2011; CLEMENS, WEILAND, 2001; WEILAND, 1996; BARTSCH, 1992). O CST MW 2011 conta com três diferentes solucionadores para alta frequência, sendo eles: O Transient Solver, utilizado ao longo desta dissertação; o Frequency Domain Solver; e por fim o Eigenmode Solver. A seguir será apresentado o mecanismo de funcionamento do Transient Solver e os demais solucionadores não serão abordados nesta seção.

Solucionador de transiente

Segundo a CST (2011), o Transient Solver permite a simulação do comportamento eletromagnético de um dado problema em uma ampla faixa de frequência com apenas uma iteração computacional. Como resultado, tem-se um solucionador rápido para a maioria dos problemas dirigidos, em especial para análise com limites abertos ou de grandes dimensões.

O Transient Solver utiliza os dados discretizados pelo método FIT para resolver a análise do problema proposto, substituindo as derivadas temporais por diferenças centrais produzindo a formulação explícita para o caso de perdas:

Com base nas relações referidas destas equações, os valores são obtidos através dos valores de tensão elétrica e fluxo magnético, sendo inicialmente desconhecidos e podendo ser calculadas alternadamente no tempo pelo método leap-frog (salto de sapo), como ilustra a Figura 7.

fit09

Figura 7 – Ilustração da aplicação do método leap-frog para cálculo dos potenciais elétricos e fluxos magnéticos no domínio do tempo (CST, 2011).

Esquemas de integração explícitas no domínio do tempo são condicionalmente estáveis. O limite de estabilidade para o intervalo de tempo Δt pode ser obtido pelo critério Courant-Friedrichs-Levy (CFL) como segue (CST, 2011):

fit10

E assim é que são projetadas as antenas nos dias de hoje.

Referências

[1] IEEE Transactions on Antennas and Propagation, vols. AP-17, No. 3, May 1969; AP-22, No. 1, January 1974; and AP-31, No. 6, Part II, November 1983.

[2] BALANIS, Constantine A. Antenna theory: analysis and design. John Wiley & Sons, 2016.

[3] Intelbras, Twin Waterproof Radiocomunicador, disponível em: http://www.intelbras.com.br/empresarial/radiocomunicacao/twin-waterproof, acessado 22 de abril de 2016.

[4] DE OLIVEIRA, Alexandre M. et al. A palm tree antipodal Vivaldi antenna with exponential slot edge for improved radiation pattern. Antennas and Wireless Propagation Letters, IEEE, v. 14, p. 1334-1337, 2015. DOI: 10.1109/LAWP.2015.2404875

[5] SILVESTER, P. Finite Element Solution of Saturable Magnetic Field Problems. IEEE Trans. On Power Apparatus and Systems. v. PAS-89, n. 7. p. 1642-1651. 1970.

[6] CST – Computer Simulation Technology (CST) Microwave Studio (MWS) v.2011, CST of America, Inc., Wellesley MA. 2011.

[7] WEILAND, T. Time domain electromagnetic field computation with finite difference methods. International Journal of Numerical Modelling: Electronic Networks, Devices and Fields. v. 9, n. 4, p. 295-319, 1996. Doi: 10.1002/(SICI)1099-1204(199607)9:4<295::AID-JNM240>3.0.CO;2-8.

[8] CLEMENS, M.; WEILAND, T. Discrete electromagnetism with finite integration techinique. Progress In Electromagnetics Research, PIER, v. 32, p. 65-87, 2001.

[9] BARTSCH, M. et al. Solution of Maxwell´s equations. Computer Physics Communications. v. 72, p. 22-39, 1992.

porDr. Alexandre

Equação de Ampère, Equação de Faraday, Equações de Maxwell

As Equações de Maxwell, o legado!

Atualmente, estuda-se o eletromagnetismo com base nos trabalhos de reformulação das equações de Maxwell.

8cngZTa[1]

Em destaque a bela fachada da biblioteca da Universidade de Varsóvia com as quatro equações de Maxwell, na forma integral, como um tributo ao legado deste brilhante cientista. Atualmente, estuda-se o eletromagnetismo com base nos trabalhos de reformulação das equações de Maxwell realizados pelos esforços independentes de Oliver Heaviside e Josiah Willard Gibbs, que se resume em um conjunto de quatro equações. A partir do estudo das equações de Maxwell pode-se descrever todos os fenômenos eletromagnéticos, a nível macroscópico (MARTINS, 1973). A primeira equação de Maxwell se baseia na lei de Faraday, a segunda equação de Maxwell, aqui apresentada, baseia-se na forma generalizada da Lei circuital de Ampère para estudo e compreensão de correntes e campos elétricos variáveis em função do tempo. Já a terceira equação de Maxwell está relacionada à lei de Gauss da Eletrostática e a última trata-se do estudo da lei básica de Gauss para o magnetismo que determina que o fluxo magnético total através de uma superfície fechada é nulo. Na sequência, vamos estudar as quatro equações de Maxwell na forma integral:

Lei de Faraday na 1º equação de Maxwell

A primeira equação de Maxwell (1), de acordo com Cardoso (2011), foi obtida pela observação da lei experimental de Faraday sobre indução magnética, que relaciona a força eletro motriz (f.e.m.) induzida (e) em um circuito elétrico fechado de comprimento total ∂A sujeito e imerso em um campo de induções magnéticas (B), com fluxo magnético (φ) variável, e com ele concatenado, como ilustra a Figura 1, que representa e=-dφ/dt.

lei_faraday

Figura 1 – Ilustração da Lei de Indução Magnética de Faraday (CARDOSO, 2011).

Esta mesma f.e.m. e está relacionada, por sua vez, à integral de linha fechada do produto escalar do vetor campo elétrico (E.) e os comprimentos infinitesimais ∂s (comprimento elementar) que constituem o circuito elétrico, o que representa o trabalho realizado por este campo para promover o movimento da carga elétrica unitária ao longo do contorno ∂A, sendo assim, a f.e.m. induzida também é igual a .

Como o fluxo magnético φ é equivalente à integral de área (integral dupla) delimitada pelo contorno ∂A, aqui denominada de área A, do produto do campo B, pela área infinitesimal de A (área elementar), ou seja, , obtém-se a primeira equação de Maxwell na forma integral:

(1)

A primeira equação de Maxwell na forma integral é o modelo matemático da relação dos campos elétricos com os campos magnéticos e vice-versa. É possível visualizar empiricamente o fenômeno representado por ela como sendo um campo magnético variando no tempo e provocando uma queda de tensão em torno de um circuito. Quanto maior for a taxa de variação deste campo magnético, maior será a queda de tensão (força contra eletromotriz).

Lei de Ampère na 2ª equação de Maxwell

A segunda equação de Maxwell (2) é formulada com base na lei circuital de Ampère, onde originalmente relaciona o fluxo elétrico total e a circuitação do campo magnético induzido B. As correntes elétricas concatenadas ao longo do comprimento do contorno fechado ∂A induzem o campo B em todo circuito ∂A. Este circuito elétrico está imerso em um meio com permeabilidade magnética dada por uma constante de proporcionalidade, aqui denominada por μ. Esta relação é representada matematicamente pela integração fechada no circuito ∂A do campo B na totalidade dos comprimentos infinitesimais (comprimentos elementares) ds deste contorno, que é equivalente ao produto da permeabilidade μ e à somatória das correntes elétricas (i_t) concatenadas a ∂A, ou seja .

Entretanto, para que seja possível realizar uma análise livre do inconveniente da variação da permeabilidade em função do campo B, pode-se expressar a lei circuital de Ampère como . Desta forma pode-se substituir a razão do campo B e a permeabilidade μ, pelo vetor de intensidade magnética H, ou seja, H=B/μ. Sendo assim, é possível reduzir a lei circuital de Ampère para , onde a corrente elétrica total i_t é equivalente a integração superficial (A) da densidade de corrente total J_t em cada área elementar desta superfície (dA), resultando consequentemente em , como ilustra a Figura 2.

lei_ampere

Figura 2 – Ilustração da densidade de corrente superficial (CARDOSO, 2011).

Como a densidade de corrente total J_t no meio é equivalente à soma da densidade de corrente de condução J com a densidade de corrente de deslocamento J_D, ou seja, J_t=J+J_D e sabendo que J_D é equivalente a variação em função do tempo do vetor deslocamento D, chega-se a J_t=J+∂D/∂t , o que leva a segunda equação de Maxwell para a lei circuital de Ampère:

(2)

Lembrando que a densidade de corrente de deslocamento pode ser bem caracterizada através da clássica análise da operação de um capacitor. A corrente flui pelo capacitor em regime de corrente alternada não se trata de uma corrente relacionada ao fluxo de elétrons, até porque seria difícil de ocorrer no meio dielétrico, mas sim devido ao deslocamento das eletrosferas dos átomos do dielétrico (este é o motivo do uso do termo vetor deslocamento) entre as placas do capacitor, que de acordo com Cardoso (2011), acontece devido ao fato de estarem sujeitos a um campo elétrico variável no tempo, como ilustra a Figura 3.

capa

Figura 3- Efeito da deformação do átomo do dielétrico sobre exposição ao campo elétrico. Deslocamento da eletrosfera para esquerda. (b) Ausência de campo elétrico, vetor deslocamento nulo. (c) Deslocamento da eletrosfera para direita (CARDOSO, 2011).

Essa condição de continuidade experimental foi introduzida por Maxwell nas equações através da variação do vetor deslocamento, o termo derivada do vetor deslocamento (∂D/∂t). No caso de uma corrente constante, o campo elétrico será constante e, consequentemente, a derivada será nula, produzindo uma corrente de deslocamento também nula. Ou seja, um capacitor comporta-se como uma impedância inversamente proporcional a frequência do sinal.

Lei de Gauss na 3ª equação de Maxwell

A terceira equação de Maxwell na forma integral (3) traz o estudo da derivada da lei de Gauss da eletrostática, que enuncia que o fluxo do vetor deslocamento de carga sobre uma superfície fechada é equivalente à carga interna a essa superfície, isto é, (CARDOSO, 2011). Esta análise mostra que a integral do primeiro membro da equação representa a totalidade do vetor deslocamento de carga D na superfície fechada ∂V, para cada área elementar dA desta superfície, conforme a Figura 4(a).

Já a carga total Q, no interior da superfície ∂V, é proveniente de uma densidade volumétrica de carga total que corresponde ao segundo membro da equação de Maxwell na forma integral (3) e é obtida pela integração da densidade volumétrica de carga ρ em todo volume V, conforme Figura 4(c), no interior da superfície ∂V, para cada volume infinitesimal dV (volume elementar), ou seja, , desta forma, tem-se:

(3)

Lei de Gauss do Magnetismo na 4ª equação de Maxwell

A quarta equação de Maxwell na forma integral, conforme equação (4), onde experimentalmente observa-se que o fluxo magnético φ sobre uma superfície fechada ∂V, Figura 4, é nulo.

super

Figura 4- Linhas de campo magnético atravessando a superfície fechada ∂V.

Sendo as linhas de campo magnéticos fechadas, de acordo com Cardoso (2011), observa-se que o total de linhas que entra na superfície fechada ∂V é exatamente igual à quantidade de linhas de campo magnético que saem desta. Devido a isso, pode-se representar esse experimento matematicamente com a quarta equação de Maxwell na forma integral:

(4)

Essa equação deriva do fato de que as linhas de campo magnético não possuem início nem fim (tecnicamente expressos como “fontes” e “sorvedouros”). Ou seja, não existe o chamado monopólo magnético, que teria carga individual Norte ou Sul, diferentemente das cargas elétricas que possuem cargas individuais positivas ou negativas.

Referências

CARDOSO, J. R. Engenharia Eletromagnética. São Paulo: Elsevier Editora Ltda, 2011. ISBN 978-85-352-3525-8.

MARTINS, Nelson. Introdução à teoria da eletricidade e do magnetismo. Edgard Blucher, 1973.

porDr. Alexandre

Gibbs, Heaviside, Marconi, Maxwell, Tesla, William Rowan Hamilton

De Maxwell, Heaviside e Gibbs, à evolução contínua do Eletromagnetismo.

maxwell Cambridge, 1863, Inglaterra, um notável físico britânico e professor de física experimental espanta o mundo acadêmico ao demonstrar teoricamente a provável existência das ondas eletromagnéticas. Seu nome? James Clerk Maxwell!

Seus primeiros trabalhos na área de eletricidade e magnetismo, nessa época, utilizavam o formalismo de componentes. Anos mais tarde, toma conhecimento da teoria dos quatérnions, que representa matematicamente vetores, e passa a aplicá-la para fundamentar matematicamente seus estudos com base no conceito de espaço euclidiano, uma vez que no tempo de Maxwell, os conceitos de análise vetorial não estavam bem desenvolvidos (SILVA, 2004).

E a teoria dos quatérnios? Bem, a teoria dos quatérnions foi proposta por William Rowan Hamilton em 1843, aos 38 anos de idade. Hamilton, retratado na fotografia de parte de uma escultura de areia feita pelo artista Daniel Doyle (Ref.), Hamilton era um brilhante cientista, tornou-se professor de astronomia e membro da academia real da irlanda. Com apenas nove anos já falava treze diferentes línguas. Hamilton, segundo Doyle, enquanto caminhava com sua esposa, teve um insight, parou e passou a formular sua teoria nas paredes da ponte de Broom. Sua teoria é amplamente utilizada na contemporaneidade para realizar rotação de vetores em três dimensões em computação gráfica, visão computacional, robótica, navegação, dinâmica molecular, trajetórias orbitais e textura cristalográfica (KUNZE e SCHAEBEN, 2004). Anos mais tarde Maxwell demonstrou grande interesse pela teoria dos quatérnions de Hamilton através do estudo dos trabalhos de seu grande quater amigo Peter G. Tait, um dos mais proeminentes teórico quaternionista, e que mais tarde, em 1867, publica seu trabalho intitulado An Elementary treatise on Quaternions.
A teoria dos quatérnions de Hamilton tem relação com seus esforços para estudar os números complexos pela representação geométrica vetorial (SILVA, 2004; HAMILTON, 1969).

O próprio Maxwell acreditava que a criação dos quatérnions era tão relevante para o estudo do espaço quanto os trabalhos de Descartes, que deram origem às coordenadas triplas. Com base nestes estudos, anos mais tarde, em 1870, Maxwell publica seu Manuscrito sobre as aplicações dos quatérnions no eletromagnetismo onde, por exemplo, ele aplica o operador a função escalar F, denominando-a como slope, e uma função vetorial σ, cujo resultado se constitui de uma parte escalar, que chamou de convergência e outra parte vetorial, ao qual chamou de rotacional (MAXWELL, 1873).

tratado A divulgação da teoria de quatérnions, que inspirou a discussão sobre esse formalismo por proeminentes físicos e matemáticos da época, se deu graças à obra de Maxwell chamada Treatise on Eletricity and Magnetism, publicado na forma de livro em 1873 (MAXWELL, 1873). O uso deste método em seu livro acabou despertando um interesse particular em dois pesquisadores notáveis que, em 1884, apresentam trabalhos independentes que resultaram na representação vetorial moderna das equações de Maxwell que conhecemos hoje. São eles: o matemático inglês Oliver Heaviside e o físico estadunidense Josiah Willard Gibbs.

Três anos mais tarde (1887), um jovem físico alemão e professor de física chamado Heinrich Rudolf Hertz inicia seus estudos relacionados à propagação de ondas eletromagnéticas (ondas de rádio) na Escola Politécnica da Universidade de Karlsruhe, Alemanha, utilizando um simples spark-gap transmitter para lecionar fenômenos eletromagnéticos a seus alunos. Seus estudos conduziram à criação de aparelhos emissores e detectores de ondas de rádio que foram usados para demonstrar a existência de onda eletromagnética previstas nas teorias de Maxwell.

Apenas sete anos depois, um jovem cientista italiano chamado Guglielmo Marconi toma conhecimento dos estudos de Hertz, e tem acesso a dezenove patentes de Nikola Tesla, um notável engenheiro eletricista croata radicado nos EUA. Marconi, ao estudar o artigo de Hertz, publicado em um jornal científico, e as patentes de Tesla, inicia seus esforços para o desenvolvimento de um sistema de comunicação, mais tarde conhecido como telegrafo sem fio.

Em pouco tempo, o sistema de comunicação de Marconi estava enviando código Morse de seu laboratório que, após aumentar a potência e o ganho da antena, conseguiu transmitir em 1901 a primeira comunicação através do oceano Atlântico. Embora Marconi seja considerado por muitos como pai do rádio, em 1943 o Supremo Tribunal dos Estados Unidos, creditou a Nikola Tesla o mérito como inventor do rádio.

Simultaneamente aos esforços de Marconi e Tesla, o cientista brasileiro Roberto Landell desenvolve estudos de telecomunicação por ondas de rádio, sendo considerado como pioneiro nas transmissões de voz humana através de um enlace de rádio frequência e tendo suas patentes depositadas tanto no Brasil como nos Estados Unidos da América. No Brasil, Landell obteve o depósito da patente 3.279 de março de 1901 e em outubro de 1904 nos Estados Unidos da patente número 771.917 sob o título de Transmissor de Ondas, em novembro de 1904 das patentes 775.337 para o “Telefone sem Fio” e 775.846 para o “Telegrafo sem Fio”. Em 2011, ele recebeu a honra máxima brasileira tendo seu nome inscrito no Livro dos Heróis da Pátria.

Em paralelo, Nikola Tesla, que em 1894 já havia demonstrado a possibilidade de se transmitir sinais de rádio frequência, apresentou em 1917 os fundamentos que estabeleceram os conceitos primitivos para medida a distância por ondas de rádio ao relacionar frequência e o nível energético. Desde o início da aplicação das teorias de Maxwell sobre as ondas eletromagnéticas, duas aplicações se destacaram: a transmissão de informações na forma de ondas de rádio e a medida de uma certa distância por ondas de rádio, que ganha grande atenção e relevância na segunda guerra mundial. Naquela época, muito se pesquisou sobre detecção e medida da distância via rádio ou na língua inglesa, Radio Detection And Ranging (Radar), impulsionado sobretudo pela fragilidade britânica a ataques aéreos alemães.

Ao final da segunda grande guerra, tanto o radar como as comunicações por ondas de rádio foram amplamente empregados na corrida espacial durante o período da guerra-fria (1957 a 1985), rivalidade entre as duas superpotências que emergiram daquela guerra.

Após sete décadas do início dos estudos de H. Hertz, Ross (1973), pesquisador da Sperry Rand Corporation, retoma com empolgação os estudos de ondas de rádio pulsantes de Hertz e propõem a primeira formulação conceitual sobre pulsos com espectro de frequência de banda ultra larga, ou do inglês ultra-wideband (UWB). Como resultado de suas pesquisas, surge o projeto de um sistema de comunicação (transmissão e recepção) através de pulsos de curta duração e livre de portadora a partir de modelos eletromagnéticos no domínio do tempo.

Durante os sete anos seguintes ao trabalho de Ross (1973), estes conceitos eram conhecidos pelo termo “carrierless” ou tecnologia de impulso. Só após este período, especificamente na década de oitenta, o termo UWB foi cunhado para aplicações de pulsos de rádio frequência ultracurtos (na ordem de pico segundos) e vem sendo utilizado até os dias de hoje.

Diferente de antenas diretivas de banda estreita, cujas dimensões não são baseadas em um comprimento de onda constante, para sistemas UWB há um tipo de antena que possui um radiador na forma de abertura, muitas vezes exponencial, e que teoricamente promove a radiação de ondas eletromagnéticas de maneira diretiva e com grande largura de banda. Esta notável antena é planar, leve e de simples construção e se chama antena Vivaldi (GIBSON, 1979; GAZIT, 1988).

Referências

GAZIT, E. Improved design of the Vivaldi antenna, IEE Proceedings, v. 135, n. 2, p. 89-92. 1988.

GIBSON, P.J. The Vivaldi Arial. In: IEEE 9th European Microwave Conference, Conference Publication. p. 101-105. 1979.

HAMILTON, W. R. Elements of quaternions. New York: Chelsea Publishing Company, 1969.

KUNZE, Karsten; SCHAEBEN, Helmut. The bingham distribution of quaternions and its spherical radon transform in texture analysis.Mathematical Geology, v. 36, n. 8, p. 917-943, 2004.

MAXWELL, J. C. Treatise on Electricity and Magnetism. v. II Oxford: Claredon Press, 1873.

SILVA, C. C. A escolha de uma ferramenta matemática para física: O debate entre os quatérnions e a álgebra vetorial de Gibbs e Heavside. In: Filosofia e história da ciência no Cone Sul: 3º Encontro. 2004. P. 115-126. ISBN 85-904198-1-9.

Laboratório Maxwell

Categoria Maxwell

#LABMAX tem trabalho de pesquisa PREMIADO no ENCOM 2016

Trabalho de pesquisa do Laboratório Maxwell, baseado em uma melhoria da antena Palm Tree, foi premiado como um dos melhores trabalhos apresentados na última edição do ENCOM 2016, que é o Encontro Anual do Iecom em Comunicações, Redes e Criptografia.

ARTIGO COMPLETO

Curtir isso:

Início do Curso de Extensão de Eletromagnetismo Aplicado no próximo dia 21

Curtir isso:

Episódio Piloto do estudo aplicado do Eletromagnetismo

Diga-nos sua opinião sobre esse episódio piloto.

Curtir isso: